

回想不多久以前,一片CD頂多只能聽70多分鐘音樂,現在一個隨身碟卻能輕鬆灌入十多小時的MP3或 iTune. 這其中的改進,要歸功於音樂壓縮技術。談到資料壓縮,就不得不提到近代數學有個重要的旁支,叫做訊息理論;其中的一個重要的課題,就在於探討隨機程序的不可預測性 (unpredictability)。此不可預測性,乃由「熵率」(entropy rate) 給出:
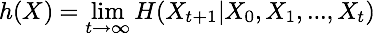
此處,h(X) 為 X 之熵率,而 H(乙|甲) 表示在甲已知的情況下,事件乙的「條件熵」(conditional entropy)。此定義式漂亮之處,在於善用了微積分中求極限的手法。 於是乎,熵率 h(X) 為程序 X 之可預測性給出了上限,而此上限必須在熟知所有歷史: {X0,X1,X2, ...} 到Xt,且 t 趨近無限大時,才能逼近。由此看來,熵率乃隨機程序的一個漸近的性質 (asymptotic property).
隨機程序的漸近性質在通信理論中有重要的應用。比如說,欲將信號源 X 作編碼,以使其資料量壓縮(data compression), 則最緊密壓縮的極限為 h(X) 位元乘以信號的長度。這就是訊息理論的「源編碼定理」(source coding theorem), 可以透過隨機程序的「漸近等分性」(asymptotic equipartition properties) 來證明。
資料壓縮在當代多媒體信號處理的應用極廣;舉凡文字、影像、聲音、或動畫,無一不須壓縮後再傳輸。比方說赫夫曼編碼(Huffman coding) 利用簡單的二元樹(binary tree), 遞迴地將最不可能發生的狀況依序映到樹的末端,於是其資料壓縮率就逼近到 h(X) + 1 以內,因此成為最廣泛使用的壓縮技術;就連現在人手一台的 iPhone或其他智慧型手機, 其音樂格式中,都運用到赫夫曼的編碼、解碼原理。
然而音樂壓縮,最關鍵的技術倒不是赫夫曼編碼,而是在於將二十世紀中葉以降,聲覺心理學 (psychoacoustics) 的研究發揚光大。實驗證實,相近但不同頻率的聲音傳入耳內以後,交互作用而產生了彼此抑制的效果 -- 這是一個弱肉強食的世界,只有較強的音源取得觸發神經的優先權。反應在知覺上,就造成了強音對弱音的遮蔽效應 (masking). 本演講將簡介遮蔽效應的生理學基礎,並說明遮蔽效應何以能幫助音樂壓縮軟體,達到接近一比十的壓縮效率。